Navigating the Waters of Investment Returns Amidst Cash Flows
Unpacking the Subtleties of Return Calculations with Cash Movements
Calculating your investment returns seems straightforward at first glance – just pit your current value against your initial investment, right? But throw in multiple contributions and withdrawals over time, and suddenly, you're in a maze. Let's talk about adjusting your starting line with those twists and turns.
When Withdrawals Stir the Pot
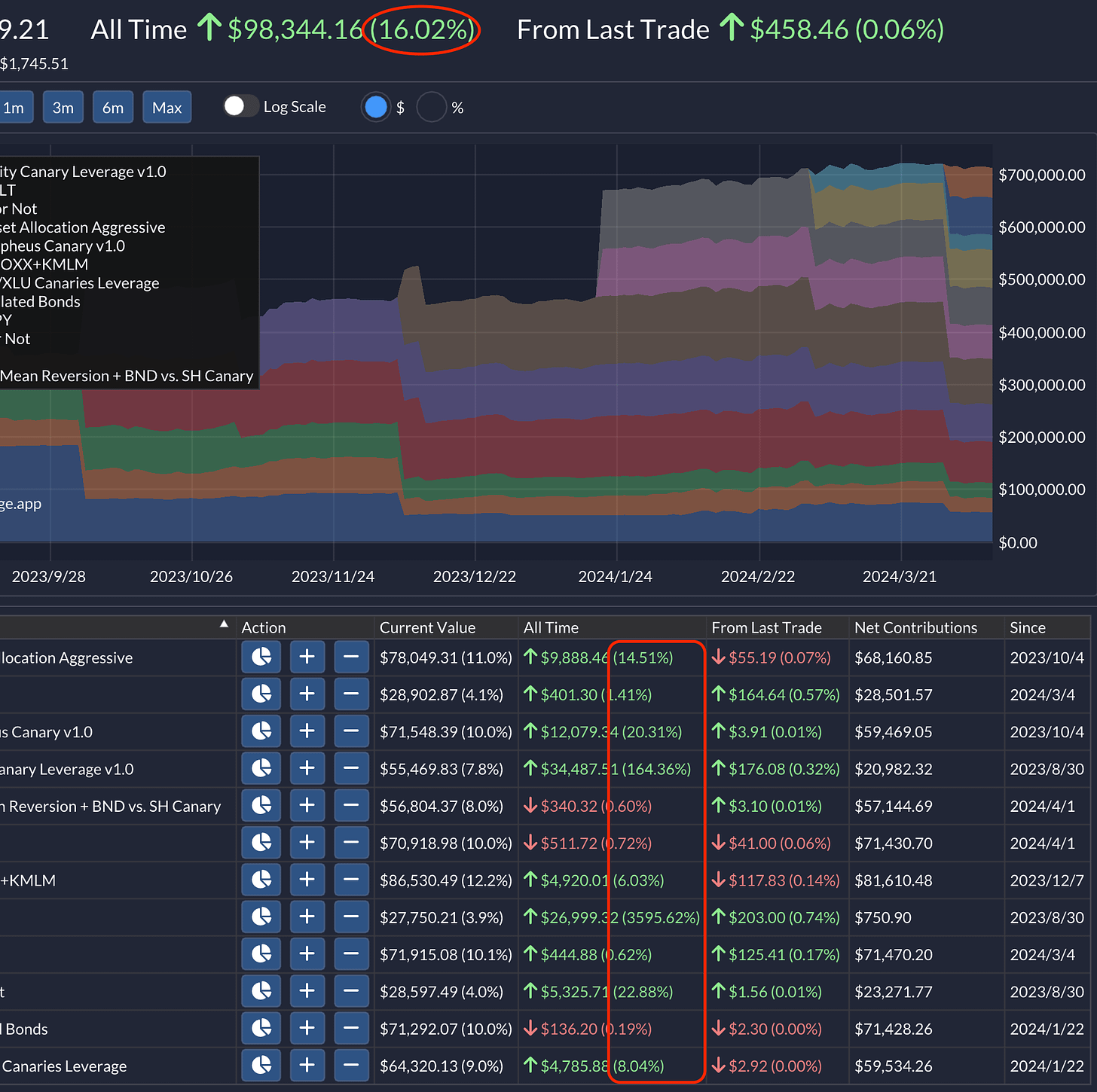
A straightforward method is to tweak your initial investment by factoring in additional deposits and withdrawals. It makes an intuitive sense. You just use the resulting net cash flow as the denominator in computing a return. But, there's a catch. Imagine your investment doubling, and you decide to take some off the table, more than what you started with. Your net cash flow dips into the negatives. Once it hits zero or below, you're staring at a return percentage that might as well be a mirage. And, every withdrawal inflates your return figures since it shrinks your denominator, giving you a distorted view of your investment's performance. For instance, let’s say your initial $100 investment grew into $200, granting you an exciting 100% gain (= ($200/$100 - 1) * 100%). Now you withdraw $50 to pay the tax, which decreases the net cash flow to just $50 (= $100 - $50) and your gain suddenly inflates to 200% (= ($150/$50 - 1) * 100%) with no price change! Another downside is that it ignores the time value of your money. $100 in your pocket now should be worth more than $100 one year later, for example.
There's a workaround for the first catch, though. Instead of yanking the entire withdrawal from your principal, consider doing it proportionately from both your initial stash and the gains. This keeps your return steady, regardless of withdrawals, ensuring your denominator never plays hide and seek with zero. With the same example above, now you subtract one half of the withdrawal amount, $25, from the principle (the initial deposit of $100 - $25 = $75) and the other half from the gain (the gain of $100 - $25 = $75), which keeps the return at 100% as before. Handling contributions remains the same, though, and each new deposit will dilute the return in both cases. I decided to call the former approach Principal-First Withdrawal and the latter Pro-Rata Withdrawal. One downside of the latter is that it makes a portfolio rebalancing result less intuitive. In the former approach, there is no change in the portfolio return with rebalancing between strategies since the principal sum remains the same. But, with the latter, some of the gains can be recognized as cost bases as they move out of the original strategies and into the new ones with rebalancing, which will deflate the overall return. In other words, the portfolio return number can suddenly go down after you rebalance its constituent strategies with the pro-rata withdrawal.
Time-Weighted vs. Money-Weighted Returns
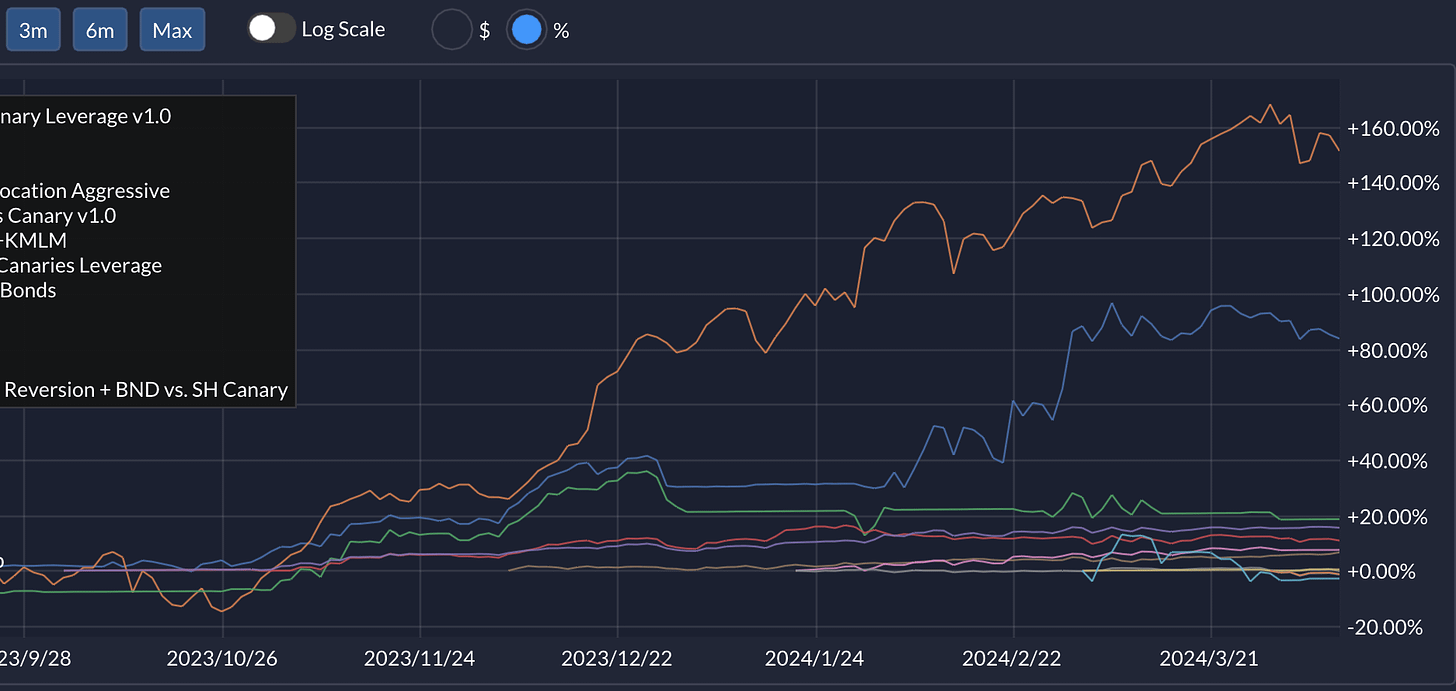
Now, for the veterans out there, you're probably itching to talk about Time-Weighted Return (TWR) and Money-Weighted Return (MWR) – two seasoned navigators in the world of investment returns. TWR just ignores any cash flow after the initial deposit and compute a hypothetical return under the assumption of no extra cash flows. In a sense, the pro-rata withdrawal approach above can be regarded as applying time weighting with withdrawals, but not with contributions. On the flip side, MWR, a.k.a. Internal Rate of Return (IRR), computes a hypothetical rate that can make all in-flows’ and all out-flows’ net present value cancel each other out when you discount them by it. Or you can think of it as the interest rate of a fixed-rate account that can give you the same return if you apply the same sequence of cash flows to it. It’s one sensible way to take the time value of money into consideration when assessing an investment return. Unlike the other returns mentioned so far, it’s impractical to manually calculate it, though.
Admittedly, wrapping your head around these concepts is no small feat. But once you do, you'll see the landscape of your investment returns through a new lens. This (pdf) can be helpful for furthering your understanding. TWR is often used for assessing the performance of an investment whose cash flow is more or less random and not in the manager’s control and when you’d like to focus on the strategy’s pure compounded rate of growth regardless of cash ins and outs. MWR can be more appropriate when cash flows can be discretionary and you’d like to evaluate their timings as a skill, too.
Charting the Course Forward
Anything incorrect or missing? I don’t think I’m at the end of this rabbit hole yet. So please guide me if you have any idea on where I should dig deeper. Well, in the realm of investment returns, there's no one-size-fits-all. Each method we've navigated today offers a unique perspective, tailored to the ebbs and flows of your investment journey.
At QuantMage, we're currently charting the course with both a pro-rata withdrawal return and a time-weighted return for each strategy, providing a holistic view of its performance. For the entire portfolio, it shows a return based on the total cost basis, which is the sum of the cost bases of its individual strategies with the pro-rata withdrawal. But, the winds of change are ever-present, and our approach may evolve as we continue to sail the vast oceans of investment strategies.
What's your compass pointing towards? Do you prefer the simplicity of the straightforward principal-first method or the shrewd pro-rata, or does the pure TWR or the nuanced perspective of MWR resonate more with your investment philosophy? And, does your preference shift when steering the ship of algorithmic and systematic investment?